A Group Test after the Test...Here's How It Went

I tried something that I learned by reading a conversation on Twitter this summer.  I would only be guessing at who was having this conversation, so if you read this and it sounds familiar, let me know so I can give you credit.  Anyway, the conversation was about tests and retesting.

What I found interesting was the idea of retaking the test as a group the day after they take the test individually.  The group has limited time, say 15-20 minutes, to complete the test.  I tried this with our first skill quiz in Algebra this year.

My reasons for trying it were to:
1) help students see that they are not the only ones with a question,
2) allow peers to work together and think through the quiz, 
3) to give me and opportunity to listen to how students were explaining the math to each other, and
4) to make sure that everyone had a copy of the quiz in their math binders with the problems worked out (some students will never bring back the signed test to put in their binder).

I have two completely different groups.  My first group is a higher ability group that doesn't enjoy being quiet and still for more than 10 seconds.  This has been a challenging group so far.  My other group is quieter, but as a group, they struggle a little more to understand the material.  They present a different type of challenge.

I say this because there were two different outcomes for this activity.  In my first group, I walked away feeling "meh" about the process.  It took a lot of work to get them started and on task, even with regrouping them so that students that did well were placed with students who didn't.  They were also more argumentative with each other in a nonproductive way.  I struggled to convince them of the value of their work.  We will try this again on another quiz/test, but I am thinking to take it another way.  I am thinking of making it an error analysis activity and using mistakes that students actually made on the test.

My second group had a totally different experience.  They got right to work, helped each other, and talked about the questions.  I heard thinks like "I thought you had to..." and "But why wouldn't you..." while they were working with each other.  This was completely beneficial for them.  I also was able to answer questions that stumped the entire group, which made for a great dialog between the students and I.  I felt like this group walked away with understanding of what they did wrong and what still needed more practice.  It was a good use of time and we will try it again in the same way.

In sharing this technique, others thought that I should do this before the quiz/test.  I don't think that it is a bad idea by any means, however I have two concerns.  My first concern is that the only way that they will review for the test, will be the group test.  I want them to know how to study for math without me giving them questions.  The second concern that I have is that the questions are standards based and more open ended.  I am a novice at writing questions this way and am just not confident I can write three or four questions that I really like, so I can do a practice test, test, and re-test.  I'm not ruling it out, but I'm just not ready to go there, yet.

Some Thanks...

The teacher workshops are completed, the room is set up, and the lessons are written.  It has been a long and exhausting week, but for the first time in a long time, I am feeling calm going into the school year.

This sense of calm comes from so many people who probably don't even know that they have helped me over the summer tie some loose ends together, rethink how and why I do things, and help me realize that all of us have the same issues in the classroom.  Everyone has the student who won't stop talking.  It's not just me.  Through the stories that they have shared, I have begun to feel that I'm not alone when I feel like I am swimming upstream.  So I want to take a moment as my school year begins to thank some of them.

First of all, I want to thank those who inspired my classroom bulletin boards this year.  Thank you for inspiration when I had none.

My favorite is the Star Wars themed growth mindset posters from Paul's (@TeacherPaulP) blog TeacherPaulP which I combined with Sarah's (@mathequalslove) idea, from her blog Math=Love, to put up sayings from a fixed and growth mindset.  I added Darth Vader and Yoda to the mindset phrases to keep the theme.  I will enjoy saying "Use the Force" this year when I hear fixed mindset statements.  

Next, I have to thank, Sarah (@msrubinteach) from Everyone's a Genius for the idea to do the loop-da-loop for how you learn a skill.  Looking forward to using it to remind students that learning is a process.  

Finally, Pam's (@pamjwilson) blog, the radical rational, had an awesome bulletin board for displaying sentence starters that I totally just did my best to recreate.  I am hoping that this will be well used by my students!

Besides all of the help with decorating, I need to also give some thanks to The Global Math Department for the truly awesome professional development that I attended this summer.  If you haven't attended a Global Math Department webinar yet, please try one.  It's free and that is every teacher's favorite word! 

MTBoS and everyone I met and worked with at Twitter Math Camp are awesome.  I am excited to become more and more involved with the both groups.  It is amazing how technology in general has made it possible to sit on my couch and talk to teachers all across the country.  I feel like I dated myself with that statement, but it's so true!

And speaking of sitting on my couch, I want to thank those who monitor the chats on Twitter.  I like to lurk during #msmathchat and Justin (@JustinAion) and Adrienne (@shlagteach) do an awesome job.  I know there are other groups and other monitors, but I haven't explored all of them yet! 

Thank you to everyone for your inspiration and willingness to share what you do! 

Behavior Expectations: My Only Summer Craft :(

This is going to be a short and sweet blog post because tomorrow is the first day of teacher workshops for the new school year and I have to start winding down and going to bed at a decent hour.  But I wanted to share one of the only craft projects I did for my classroom this summer (which I did today). 

I have been feeling like a grinch because I have had little enthusiasm to decorate my room.  I want it to look pretty, but really wish my fairy godmother of the classroom would come and wave a magic wand.  Then my room would be the prettiest in the land.  OK, enough wishful thinking.

I wanted to frame my expectations (ok, not really mine; borrowed from another school I used to teach at a few years back) and put them on the wall.  I went to my local craft store, but the $1 frames were to small and the others too expensive.  I thought about misscalcul8's blog and this picture.  I thought that I could get some scrapbook paper and laminate it.  I had found cute clothes pins at the craft store, so it seemed simple enough. 

Well, half way through picking out scrapbook paper, I decided that I wanted something sturdier.  I went back to get some foam board and found packages of 8"x10" foam board.  Problem solved!  I bought the foam board and the scrapbook paper and headed home to make something pretty for my classroom.

This is what I created.  Scrapbook paper and foam board are now my new best friends.  I am very excited and think that they will look great in the classroom.  Plus, they will be a visual reminder to the students. 

If you want to know more about the behavior expectations, here is a link to the parent handbook from my previous employer.  I don't use them exactly the way they are prescribed in this handbook. 

Goals for 2014-2015 Academic Year

I go back to work on Monday for teacher workshops and getting the classroom ready for the new school year.  I have been lacking motivation to go and spruce up my room this year and I know that I will have a lot of work.  Fortunately, I did not have to take everything down off of my walls and bulletin boards.  So, it is more about trying to make the room look fresh for the new school year and I have plenty of ideas to make the freshness happen. 

Each year that I have worked with my principal, he has asked for the staff to write their personal goals for the academic year.  I have been working on what mine will be.  I've narrowed it down to theses three:

1) Blended Classroom:
At the end of last year, I felt that the goal for next year was going to be flipping the classroom.  That is still a goal, but it will be much more of a blended classroom than I originally thought it would be.  There are a lot of reasons for this. 

The biggest factor to sway me is that I am going to "unit-fy" the Saxon Algebra I book.  I found that as I "unit-fy" the text, there were places that I could actually give myself time back.  I especially found that there were lots of places to make a foldable that contained ideas from several lessons from the text. 

I will still make tutorial videos for students throughout the year.  I will also assign some of them.  I am just not quite ready to be fully flipped.  Maybe that will change as the year progresses.

2) Standards Based Grading:
I want to make strides to do this better this year.  I have spent a lot of time matching units, lessons, and standards and melding them together to hopefully be cohesive.  I have developed a self tracking sheet for students to keep in their INB this year.  I started units in Jumprope (it's a free on-line SBG grade book).  Still playing with the grade book and will see how it works.  I like the reports that it will make for me.  I think it will help parents transition into SBG.  I am also in the process of making syllabi for each unit.  All of this has meant less time for making foldables and putting together INBs.

However, none of this will work well unless I am more diligent about getting the corrected work back to the students.  Feedback is an area I have struggled with my entire career.  I need to improve and by focusing on making standards based grading work, feedback has to be timely.

3) Less Time Explaining; More Time Doing:
My last goal ties into the blended classroom.  I want to spend more time doing math and talking about math.  I have already gotten a subscription to Mathalicious and I want to subscribe to Yummy Math.  Both sites have lots of interesting problems, are real life based, and are very, very reasonable for the teacher budget.  Especially, if you are like me and will be paying out of pocket to access them.  

I want the students to do more thinking which means I really need to keep the classroom focused on collaboration.  I am hoping that the problems I find on both of these sites (and others sites I find throughout the year) will help me to foster that collaborative feeling.  Time will tell.  Plus, I can plan all I want, but until I have students in my room trying to do these activities, I won't know.

Well, those are my three goal.  I think that is enough.  I also feel like I will be able to measure them by the end of the school year.  Success is hopefully in my future!

Integer Word Problem Practice with My Twist

I have been procrastinating by digging through my folder on my desktop labeled, "7th Grade Math".  Clever, huh?  I came across some integer problems in there that had a lot of promise as in-class practice.  It was a freebie that I had downloaded awhile back and it took a little research to find the author.  Anyway, I found that it came from Lisa at Teacher's Notebook.  I really liked the problems that were on the worksheet, but I was bummed that it was a worksheet.  There had to be a way to rework it, so that it would be more intriguing to my middle school kiddos.

photo credit: www.ew.com

I started thinking about the old game show from the 80s, "Classic Concentration".  If you haven't seen the show, contestants make matches on the game board to win prizes and slowly uncover a puzzle.  The person who solved it got a bigger prize. (See sample to the left)

Since the worksheets eventually lead students to do a coloring sheet, I thought that maybe I could use the idea of uncovering a puzzle. 

The first thing that I did was take the answer sheet and resize it to be 20 cm by 25 cm.  I then printed it out and glued it to a piece of card stock.

Next, I made a 5 x 4 grid.  Then I wrote the 12 correct answers in the boxes and 8 incorrect answers.  All of the solutions and incorrect solutions came from the answer key.

Then I cut it apart into 25 separate squares. 
                                                              

So this is the starting point of the activity.  I have the template for the answer sheet that students fill in at the end of this post.  The basic idea is that students would start like the above picture.  As they solve a problem, they will look at the board and then flip over the piece with their answer.  If they don't see their answer, they will need to check their work for errors.

As students continue to solve problems and flip over pieces, they will start to see the pieces of the answer sheet in the incorrect order.

Students will also realize that there are 8 unused answers.  Students will be asked to write a question/problem that has the unused answers as an answer.  

After the questions/problems are written, all of the pieces can be flipped over.  Students then have the job of getting the pieces into the correct order and making the picture.

The students' pictures will look like this when they are finished!

OK, so it's not exactly "Classic Concentration".  While making this activity though, I did have a few thoughts about how to make another activity that would resemble the actual game more.  I'm working on that one!





Here is the answer template that the students will be completing during the activity.  Before the activity, I would type in the questions from Lisa's worksheet or I am thinking to change "Problem" to be "Important information to solve the problem".  Then, I could just pass out the questions or put them on index cards.  

First Page of This Year's INB!

Now that there are only two weeks until teachers have to report, I have officially decided that it is time for me to begin panicking and get some stuff started and other stuff finished.  I started to put together my INB for my algebra class.  I only have a very rough start and will share when I get a few more things in it.  Some foldables are still in prototype phase and all the kinks are still being worked out of them! :)

I did however get the first page finished and I am really excited about it.  I originally decided that I would have the first page of the students notebooks be a "Math about Me" page and I went to my trusty friend, Google, to find some images for inspiration.  Most of the ones I had seen were for elementary grades.  Then I came across this one that was posted on "Shut the Door and Teach".

Template available at TPT. 

I really liked that the students made expressions that went with the numbers that were about them.  I really loved that it connected to our second topic of the year – order of operations!  I am still working the plan out, but I think we can spend some time double checking each others' "Figure Me Out" page as a warm-up or practice activity. 

The example above was for fourth grade, so I needed to put some guidelines in place for my middle school students.  In the directions, I said that they needed to use fractions, parentheses, exponents, square roots, etc. to write their expressions.  The expressions had to be at least 3 terms as well, to stop 9 + 1 being the expression for 10.  I also hope that my example will inspire them to be tricky and challenging.  Here is what I did:

 

I will fill in my self portrait by the time that the kiddos see it.  I also forgot to use a square root somewhere, so I have to fix a sticky note!  The answers are under the sticky notes, so after the students evaluate the expression they can check and see if they are right.  I think it is an easy entry point for students to get back into the groove of math.

Update (8/19/14):  I didn't realize that the author of Shut the Door and Teach had a template available on her TPT store.  Due to copyright, I can't keep the template I formatted to fit in my INB available for free download.   

Tellagami for Vocabulary...I'm Still Unsure

This picture caught my eye on Pinterest a while back and I am finally getting around to checking it out.  This comes from Matt Coaty who writes the blog Educational Aspirations.  Matt teachers gifted and talented students at the elementary level.

When I first saw it, I thought what a cool idea for getting students to show multiple representations of the same vocabulary word.  After closer inspection, I realized that the students were actually showing how to solve the problem.  I thought this is brilliant and totally motivating for middle school kiddos.

Since I had never heard of Tellagami,  I downloaded the free version from the app store on iTunes to my phone.  I played with it a little bit and it is pretty simple and students would figure it out quickly.  It's nice from the standpoint that there are a limited number of choices that the students can pick, so they can't spend hours picking the outfits and hairstyles and then never get to the math.  There is the option to type in the text and let a computer voice say it or you can record your own voice.

I have finally made my first gami about slope.  To start, I made up some cards about slope.  I opened the app and selected the background, then took a picture of my cards with the little person on the screen.  Then I recorded a little something about slope. It was really that simple.

To hear it play, click here

But, there are some downsides to this app that I found as I played:
1) There are in-app purchases (boo!).

2) There is a limited trial time to access everything.  After that you are left with one type of clothing which you can change the color of the shirt/pant.  That doesn't bother me.  Losing the ability to type what the character should say and then pick a voice is a bummer for me.  I don't want to pay for it.

3) There is the cost for the educational version of the app.  The cost is $4.99/subscription.  The up-side is that there are no in-app purchases.  It's just a bit too much to ask my school to pay at this time.

4) Because of the in-app purchases, I can't have students use their phones to produce a Tellagami.

5) Students are limited in the free version to 30 seconds.  I believe it is reasonable for a vocabulary word, but might not work to explain a problem.

6) There just isn't an easy way to collect them and put them into a file for later that I can figure out.  The email depended on the email entered into the device.  We can't use Facebook or Twitter for good reason from our school devices.  The only other option to share is via text.  That is how I was able to link my screen shot to the gami that was made.  So, timing is vital if students create these.  We need to share them during the same class period.  Or, one day is for planning and another day is for recording/sharing.  

I know that my students would love it.  But I am not sure after playing with it.  So I started thinking of alternatives.  Since my students enjoy making videos, we could do it without the Tellagami app and just record a video and save it to Google drive.  We would loose the computer animated person though and I know that would be novel and intriging.  They could make their own figure and insert it into the video.  Ultimately, the idea that Matt wrote about on his blog can be adapted.

I am putting this out there, hoping, that maybe there is someone wiser than I, who can tell me other options to work around the downsides of the app.  Does anyone use Tellagami (or something similar) in their classroom?  What do you do with it?  Love to hear about it! 

Ratio Fill Up (Ratio/Fraction Equivalences)

Here is another game from TMC14.  This is the game that my group worked on so I can take some credit in it's creation.  My group's goal was to create a game about ratios/proportions.  We were thinking of ratio tables and wanting students to see that each ratio was equal to the other.  There are quite a few rules to this game as you can see.  I took the rules straight off of the TMC14 wiki.

Objective: To earn three points [counters] by filling ratio tables with congruent ratios.

Materials: Gameboard with 4 ratios tables with room for 5 ratios in each table,  ratio cards, point counters, calculator.

Set-up: Shuffle ratio cards and deal 5 to each player.

Game play:
1) The first player plays any ratio card from their hand in the blank first space in a ratio table and then draws a card to end his/her turn.
2) The second player can either play an equivalent ratio in the same table as the first player or play a different ratio in one of the empty tables.
3) Play continues with each player playing equivalent ratios to fill up the ratio tables and drawing cards to replace the ratios just played.
4) When a ratio table gets full, whoever played the last ratio into that table gets 1 point, as long as they can identify operations to get from the first ratio played to the last (ie, if the first ratio is 2/8 and the last is 4/16, they could say multiply by 2/2 or divide by 2/2 and multiply by 4/4).
5) The player to the right of the player that played the last ratio will take the calculator and divide out the ratios in order to check to make sure the ratios are all equivalent.
6) Cards from the completed ratio table are put into the discard pile, and the cleared ratio table is open for any player to play in.
7) The first player to 3 points (counters) is the winner.

Other rules:
1) If the draw pile ever runs out, reshuffle the discard pile to create a new draw pile.
2) If a card is played incorrectly the player that noticed the error draws an extra card and the incorrect card is put into the discard pile.
3) Skips, reverses and wilds:

• Skips automatically skip the next player, 
• Reverses switch which order the players play (so, if play is going left at first, it instead goes right), and 
• wilds can be played in any ratio table that already has a ratio in it, but the player who plays it must name an equivalent ratio that isn't already in the table.  

4) If none of the cards from a player's hand can be played on their turn, that player discards one card and draws one card and their turn ends.

OK, this is a lot of rules!  Our group did agree that the game still needed some tweaking, but we just ran out of time.  Also, I am not so sure about the 4th rule.  I'm having trouble seeing the value in doing that.  Maybe when I play it with students I will, but right now I am struggling.  I would rather have my students identify the pattern in the ratio table and figure out how to do that considering that the ratios are not placed in any specific order during play.  What strategy would they use to figure out that there is a scale factor of 2/2?  What discussions or debates would come out of this?  Sometimes the first and last ratios played don't display an easily identifiable pattern and for the lower students, this could cause frustration.  I'll just have to play it and see.

Another thing that I did to modify this was to add labels to the ratio table.  I just felt like if students saw the labels they would not be thinking fractions.  The Power Point below is completely editable, so if you would like to remove those or change them, it is possible. 

Below you will find the gameboard and cards that I made up to use with my students.  The cards are ment to be cut out like fractions.  A more challenging option would be to cut the individual numbers apart and have the students work together to make ratio tables that are true and to explain how they know they are correct.  There is definitely room for tweaking and developing spin-offs of the basic game.

If you play this with students and make modifications, I would love to hear what you did and how it worked for you!

My Closest Neighbor (Estimating with Fractions)

At TMC14, I attended the same morning session for the three days that I was at the conference.  It was a session for middle school teachers and we spent time thinking about games.

I like games in the classroom, so this intrigued me.  We started by playing games and reflecting on their value in that classroom and how we could not only use what we played, but how we could structure time for the games.  I particularly liked the game Swish.  Here is a video if you haven't heard of the game before.  It is easier to watch than for me to explain.

I liked that Swish gave students practice working with transformations without them having to have been formally introduced to them.  It was also easy to create levels of skill by telling students they could only win cards if they could do it in 2,3, 4, 5, etc. moves.  More moves means more cards, but ups the difficulty level.

After playing the games, we spent the next two days developing and playing the games we created.  If you would like to see all of the games that were created click here to go to the middle school page of the TMC14 wiki.

One of the games that I played and really liked the adaptation for was the fraction war game on the wiki.  The variation that I played involved giving each player 5 cards.  We used Phase 10 cards to play with, however, I don't have those.  I do have Uno cards, and that allows me to play with fractions that have denominators from 1 to 9.  Until I can get Phase 10 cards, Uno is a good substitute.

After every player has 5 cards, we set a goal.  We decided that the player closest to 1/2 would win the round.  To not have fights among students, I made cards for them to flip over and make their goal for that round.

As you can see in the picture, the goal was to get the closest to 1/2.  So based on my hand above, I know 2/3 and 3/4 are too big, but would it be closer than what the other players put down?  That is where I (and students) need to take some strategy.  (It also needs to be decided ahead of time if going over is OK or not.)  My other options are 2/8 or 3/8.  So I have to pick one and hope I am the closest.

Since 3/8 is closer, I would choose to play that and hope that I would win.  Now, imagine the discussion that would happen and the proof that the students would have to have if another student put down 3/7.  Which is closer?  How do we know for sure?  How can we prove it?  These are great questions for mathematical thinking and great opportunity to do informal proof and debate in the math classroom.

Now what is pictured here would not work for closest to 1/2 because 2/4 is exactly 1/2 and that isn't what the card said.  This is a great chance for students to identify equivalent fractions as well.                                                                                                               

 

I didn't develop this game.  It came from another group's game fraction war.  As we were rotating and playing each others' games, my group mate Justin thought it would be an interesting twist to try to get the closest fraction to a certain value.  We played a few rounds like that and the discussion about what was close or that exact didn't win was valuable and worth time in my classroom next year.  

All that I can take credit for is giving it a new name, "My Closest Neighbor" and making the cards on the Power Point presentation below.  I left this editable.  Depending on how good my kiddos get at this, I may need to add 6/7 or 1.2 to the mix.  I do think some decimals would be good for them to think of equivalencies and conversions.  

I am looking forward to trying this with my kiddos in the fall.  My seventh graders should enjoy it!

Frog, Log, and the Questions that Ensue...

Yep!  Tonight was one of those nights when I really needed to be pulling together my unit 1 plan for my algebra class, I found myself completely distracted.  I blame the orange flippy frog that was staring me at me on my desk and the empty toilet paper tube sitting next to it.  It was not my lack of self discipline! :) 

Anyway, I started playing with the flippy frog instead of working diligently.  I then started wondering if the frog could make it over the toilet paper tube.  I thought it was a solid experiment and worthy of exploring.  So, I did.

What I noticed was that sometimes, he didn't make it over the log.

Yet, other times he would make it.








Now, I realize that it doesn't take any great skill to know that this would happen.  It fact, a small child probably could have told me what would happen.  I started wondering if the frog was more likely to make it over the log (aka toilet paper tube) or not to make it.  I hypothesized that it would be an equally likely chance that the frog would make it over the log.  Well.. at least theoretically, it should.  The operator plays a huge role in changing the chance of the frog making it over the log.  My frog failed to make it over the log the majority of the time. 

I could use this idea for a demonstration of theoretical v. experimental probability, but I wanted more to the lesson.  So that led me to the question, at what distance is it improbable that the frog will make it over the log?  At what distance is it almost certain that the frog will make it over the log?  What then is everything in between those two distances?  Are they all capable of producing the same probability?  Where does it change?

Well, that led to another experiment.  I made a little "football" style field.  I marked lines at 1cm intervals and tried to find some answers to my questions, but I was left unsatisfied.

I feel like my students could determine a distance where it is improbable that the frog will make it over the log and where it was almost certain.  I'm not sure that the data in between those points can be determined as easily without quite a bit of experimentation and data collection.  There is nothing wrong with doing that, but I am wondering if it is an activity that will be valuable for the time that it would take.  I was playing for over an hour.  I know that we could do some group collection of data and analyze that.  There would be value in doing noticing and wondering. 

I am feeling unsatisfied by the results though, and it bothers me.  Maybe because it seems that there should be a simple answer.  However, maybe I am looking for a simple answer when their isn't one.  There is even the possibility that the experiment doesn't support what I want to know and I need to revise. I'll have to keep thinking.  Data and probability won't be until mid-year.  Plenty of time to develop, modify, or throw out this idea.

If anyone has any thoughts on any of the questions that I posed, I'd be open to hearing your thoughts.  I will be thinking about this some more.  If I develop this farther, I will post what I did and anything that I used to guide the students. 

A Final Thought on TMC...

Oh boy!  I have been reading a lot of blog posts about TMC.  The biggest discussion has centered around a post by MrKent800 entitled, "I'm a Fraud".  There is a lot of discussion about this and posts in response to it.  If you haven't read it, go and read it. 

I read the post by Mr. Kent and felt sorry for him.  I wanted to offer words to sure up his confidence, because I don't think that one conference makes you feel the way that he did.  Other things have to have been happening in his classroom and professional life.  I also empathized with him a great deal because even last year, there were times when I wanted to throw in the towel and quit teaching as well. 

The thing is, when teaching is a part of you, you cannot just turn your back on it.  Yes, you get tired – to the point of exhaustion.  But, even at exhaustion, I am willing to try one more thing.  Do one more thing.  This is because I haven't completely given up on myself.  I know that I can do better.  I can be better. 

I am striving to be the best that I can be.  I use other teachers who I work with or who I religiously read their blog, to help me define what the best is.  Each person that I was a bit star struck by at TMC has helped me to refine, shape, polish, destroy, and rebuild what my definition of best is. 

I know what my strengths are and what my weaknesses are.  After fifteen years in the classroom, I know what weaknesses probably aren't changing.  I need to find ways to counter my weakness so that it does not hold me down and keep me from changing, or at the very least, trying to change. 

As I think about TMC and consider the reflections of others, I am realizing that I can't change the world.  But, realistically I don't think I ever truly believed that I could.  I just want to help the people in my little corner of it embrace the possibility of what can be.  I don't believe that I am great at it.  I just keep talking about what I know, what I believe, what I want to create and hope to achieve by it's creation.  I don't expect miracles.  I don't even expect huge amazing changes because I have come to realize after working in many different situations that I am the only one who can change.  If others chose to follow my example, so be it.  As for me, I will continue to seek out people who inspire me, challenge me, and support me.    

Twitter Math Camp 2014 (TMC14)

Last summer, I had been blogging for about 4 months when I read about Twitter Math Camp (TMC).  I had read a wrap up post or two (OK, maybe more than that) about TMC and thought it sounded like a really cool experience.  So, I wanted to make sure that I was able to attend this year and check it out.  As a first time attendee of TMC, I wasn't totally ready for this experience and this is why:

1) No Lurking Allowed!  It's Time to Share and Collaborate!
I am such a wall flower in new situations and I like to sit back and just observe.  Well, I tried that and within the first 5 minutes of the whole event starting, one of the organizers, Shelly I believe, approached me and asked why I was standing against the wall all alone.  I was shocked by this!  I fumbled through a nervous answer.  I had never been to any other conference where people had been concerned that I was alone.  I had been to a lot of events where I could just blend into the background and not be noticed.  I knew networking and meeting people was a huge part of the TMC experience, but I had planned to ease my way into it.  Didn't happen that way and that was a good thing!  I shook more hands, exchanged more smiles, and met more people than anywhere else that I have ever gone. 

Also, I have never been to a conference where I spent three morning session blocks with the same people all three days.  This is the hidden gem in TMC for me!  This was what changed the TMC from being a conference to being a collaboration.  Teachers were creating, asking questions, defining, debating, reshaping, and collaborating everywhere.  This is how community is built – in the exchange of ideas and rallying around a common cause.  Everyone at TMC was there to learn something from each other and to support each other in making mathematics education better.  It was hard not to start talking to someone about something.  Also, it was a room full of 150 passionate math teachers and where else you sit and talk with any person in the room about math?!

2) Star-Struck and Finding New Stars!
I wanted to go to TMC partially because I had been reading the blogs of many absolutely amazing teachers.  I wanted to be able to sit and chat with them and glean their knowledge for next year.  Well, it took all of my courage to tell Sarah, from Math=Love, that I loved, loved her blog.  I have stolen, I mean borrowed, so much from her.  I sat one person away from Julie, who writes I Speak Math, at a session and couldn't tell her at all how much I enjoyed reading her blog.  Then, I had an entire session with Katheryn, from i is a number, and said nothing!  I was NOT expecting to be so tongue tied!  So disappointed that I failed to introduce myself to the people I admire and strive to emulate in my own way.  But then, you meet all of these other great people.  People that you can't believe you never knew existed and are amazing!  I know that my blog reading list has just lengthened and I am really going to have to get better at Twitter.

3) The Hotel is Like Vegas!
I didn't stay at the hotel that almost everyone else stayed.  I was traveling with my dog, so I needed to stay in a pet friendly hotel.  I didn't realize until the end of TMC, how much interaction and sharing happened in the hotel after the sessions were over.  I wish that I had know this as a first timer to TMC.  I also wish I could tell you all that went on at the hotel, but I believe the saying was "What happens at the hotel from five to midnight, stays at the hotel", so I am not any help!  Although... there are some pictures floating around that show the Twitter math campers sitting in circles sharing interactive notebooks with each other! :)

So this year, as a newbie, I wasn't ready for everything.  My biggest take-away from TMC14 is that there is a huge support system on Twitter.  These teachers are totally awesome and are collaborating to make their classrooms better.  There is no need to worry about if you are a good enough teacher or even think that you have nothing to contribute.  Besides being able to put faces to Twitter handles, I left TMC14 feeling like my classroom is moving in the right direction.  I haven't fully processed the entire experience yet.  There are speakers, sessions, and games that I want to share, but they will have to wait for another post. 

Daily Mantra

Photo credit: www.hark.com

Does anyone remember Stuart Smalley from Saturday Night Live?  He had a little mantra that he said in every skit: "I'm good enough.  I'm smart enough.  And dog gone it, people like me." I know someone read that line out loud to their computer as they read this! :)

I have been reading a lot about growth v. fixed mindset in different blogs and tweets.  The other day I was thinking about how to increase my students' growth mindset when they come in with a fixed one.  I started thinking about self affirmations.  Would having a daily mantra that affirms their ability to succeed help change students views of math and their ability to do it?

I jotted this down on the back of an index card.  I kind of like it and am seriously considering using this to start my math classes this school year. 

Today is a great day to do math!
I am a mathematician.  
I know that being fast is not the same as being smart.
I know that I am smart enough to do all of the math that comes before me.
When I struggle, I know that I have the support of my peers and teacher to work through the frustration and succeed.
I know that success is not given; it is earned through hard work and dedication.
Today is a great day to do math!

Does anyone use a daily mantra or self affirmations in their classroom?  What have you observed?  I would be very interested to hear from you!

Out With The Old...

Well, I finally decided that I am going to remove the problem solving category from my grade book.  That isn't as horrifying as it sounds.  For many, many years, I have been giving students problems that would stretch them and get them to think a bit more creatively.  This was to be done independently of class time.  Some years, it has worked brilliantly and other years it hasn't been as successful.  I just feel like this has run it's course and is time to try something new.

As my classroom transitions next year to a blended and then flipped classroom, I am realizing that I will need to differentiate much more than I am currently doing.  I also need established tasks for independent work time or for fast finishers.   What I have done in the past just won't cut it for next year.  I have also been reading a lot about standards based grading and I am realizing that I have a great opportunity to replace something that needs to be gone with something that can tell me more about my students understanding.

The one hurdle I kept running into was the book.  Saxon isn't totally designed for how my train of thought was going.  As I was flipping through the teacher pages, that I've never really read, I found a list of lesson by topic.  As I examined the list, I decided to go rogue and not follow Saxon lesson by lesson.  I know it isn't recommended, and yes, I may regret this, but it is worth a shot right now.  So I am offering my apologies to all of the Saxon Algebra I users who are yelling at me as they read this.

The beauty of freeing myself from following lesson by lesson was that I was able to create.  I started looking through an old Transition Math and CPM Foundations of Algebra, Year I textbook that I had and found some inspiration.  I put some twists on a few of the ideas to match the standards I was teaching.  Once the creative juices were flowing, I was getting more and more excited about what was appearing on the paper before me.

Here is what I created.  I am excited to use these in place of the problem solving I have been doing.  I am hoping for a richer experience for my students and myself!

Hot Topic Thursday...

My head has been spinning the last few days.  I have been trying to start organizing units for next year for my algebra class.  It has been a lot of work especially if I want to continue making strides with standards based grading and holding my students accountable for mastering the standards.  I have so many directions that I want to go and I am still working to prioritize in addition to deciding what I can actually manage.

One decision that I made about next year is that I really want to structure some specific extra help time after school.  I am thinking to resurrect "Hot Topic Thursday".  Every Thursday there was a specific topic that students were struggling to master.  I started this because I noticed that students would come for help and have no idea what to ask, even with prompting, and couldn't advocate for themselves.  I also noticed that some students were simply shy, uncomfortable, or reluctant.

"Hot Topic Thursdays" started as a way to make coming for help more comfortable for the students I described previously.  With each Thursday having a specific topic, students were able to identify topics that needed more clarification.  It helped them to be able to advocate for themselves by simply walking in the room.  I also encouraged students to bring someone with them which reduced the anxiety of being the only one.  I also told them what we were going to do, but kept it loose enough to make changes if needed, when they came.  Students knew that they weren't going to do worksheets.  We usually used manipulatives to clarify topics.

I found that more students came and brought someone else with this structure.  I was able to work with them more intensely than when we were in class and the students asked more questions.  There was a lot of piggy backing off of other students questions.  The conversation was good and students made progress.

If you are interested, here is the flyer that I sent home with students:



What structures do you use to encourage students to come in for extra help?

What's My Function?

The bottom x value is a 3.  It isn't very clear.

A few years I switched schools and in that move, lots of stuff ended up in my office area at home while it waited to go to it's new home in my new classroom.  Well, some of it never made it and after looking at it for the past 3 summers, I finally decided that it was time to dig through what was in the boxes and start organizing or throwing.

Here is a little gem that I came across in the files.  Writing the function rule from a table was a challenge for this particular class, so I had them make these cards.  Everyday, a new student posted their function table and the class worked to figure out the rule.  We then posted it for students to use for review on their own.  It was great practice, but it took a lot of time!  I think that is why is is still sitting in the file because it would impossible that I just forgot about   it! : )

I started thinking about this because I liked the premise of what I did.  So I came up with two alternatives to use instead.

1) Students would find a new partner each day and practice finding the function rule of their partner's card.  It would allow the opportunity for the students to practice coaching.  Also, it gives them an opportunity to explain their thinking and get clarification from a peer if needed.

2) Students could put the same information onto an index card.  They could do a mix 'n' match with them.  I could collect the cards and redistribute everyday and do a quick 5 minute review.  The index cards could also go into a station activity at a later time.

There are probably more ways to use this that my summer brain isn't coming up with yet.  Does anyone else have an idea of how to use this in the classroom?

What the Newbie Learned about Standard Based Grading...

So last year, I made my first attempt at moving towards a standards based classroom.  I began very small by listing the learning goals (standards) at the top of each test and then breaking the test into sections.  Each section contained only questions relating to that standard.  This is nothing new to me, but not something that I put into practice very often.  I heard about doing it years ago from my guru, Rick Wormeli, at an AMLE conference or SDE conference. (I love hearing Rick present!  He energizes and challenges me.  Go see him if you haven't!  I'll stop gushing now.)  Here is an example of what I was doing:

 

After a year of doing this consistently on every test and quiz, I learned the following three thing:

1) The test really wasn't enough to demonstrate mastery. 
In all honesty, there was a part of me that was hoping the test would be enough and I could say that standards based grading was a breeze.  Ha-ha-ha! That was a nice wish.  Next year, I have to focus on the assignments that I am giving and how they help me see what my students know.  I do a variety of activities, but I need to reexamine how I use them and why I am using them.   I am also thinking that less may be more when it comes to what goes in the grade book. 

2) My scale of 3, 4, and 5 was just renaming the traditional grades of 60-100%. 
I began to realize as the year went on that I was bringing awareness to the standards being learned, but not really standards based grading.  I need to keep working on a rubric that reflects the students' journey towards mastery.  This has been tougher to develop than I thought it would be.

3) It is hard to do standards based grading in a traditional, on-line grade book.  
I managed better than I expected, but I didn't feel a traditional grade book let me record the up and downs of working towards mastery.  I need to track this outside of the on-line grade book.  Just not sure what will work for me yet.

I am at the very beginning of standards based grading.  I plan to take what I learned and improve upon it.  Thankfully, since standards based grading isn't mandatory, I have time to develop standards based grading in my classroom.  That is a luxury I am not taking for granted. 

Algebra Zoo

It's hard to see on the picture, but the fish are Cs.

As I was cleaning out files today, I came across some pictures of the "Algebra Zoo" that students had made a couple of years ago.  I use the "Algebra Zoo" to give students a visual of why we can't combine two different variables.

The "Algebra Zoo" goes back to my eighth grade algebra teacher, Mrs. Ryan.  Mrs. Ryan was from Ireland and she had red hair, an Irish accent, and told fabulous stories.  I really liked her because she had silly stories that helped me remember important ideas in math.

Mrs. Ryan asked us one day, "What is a zoo like?" and we said the normal things like a lion, bear, giraffe, cages, animal shows, etc.  She then asked "What animals are put in each cage?"  She then went on to ask something like, "Why wouldn't you put the lions and gazelles together?" and the obvious answer was that the lion would kill the gazelle.

The dolphin forms a U!

Mrs Ryan used her metaphor to explain that trying to combine 4x and 5y was like putting the lions and gazelles together.  It would never work and wouldn't end pleasantly.  They were different creatures and they couldn't live peacefully together in the same cage.

She did stress that x and 5x were the same creature, but they looked different.  They were special and lived peacefully in the same cage.

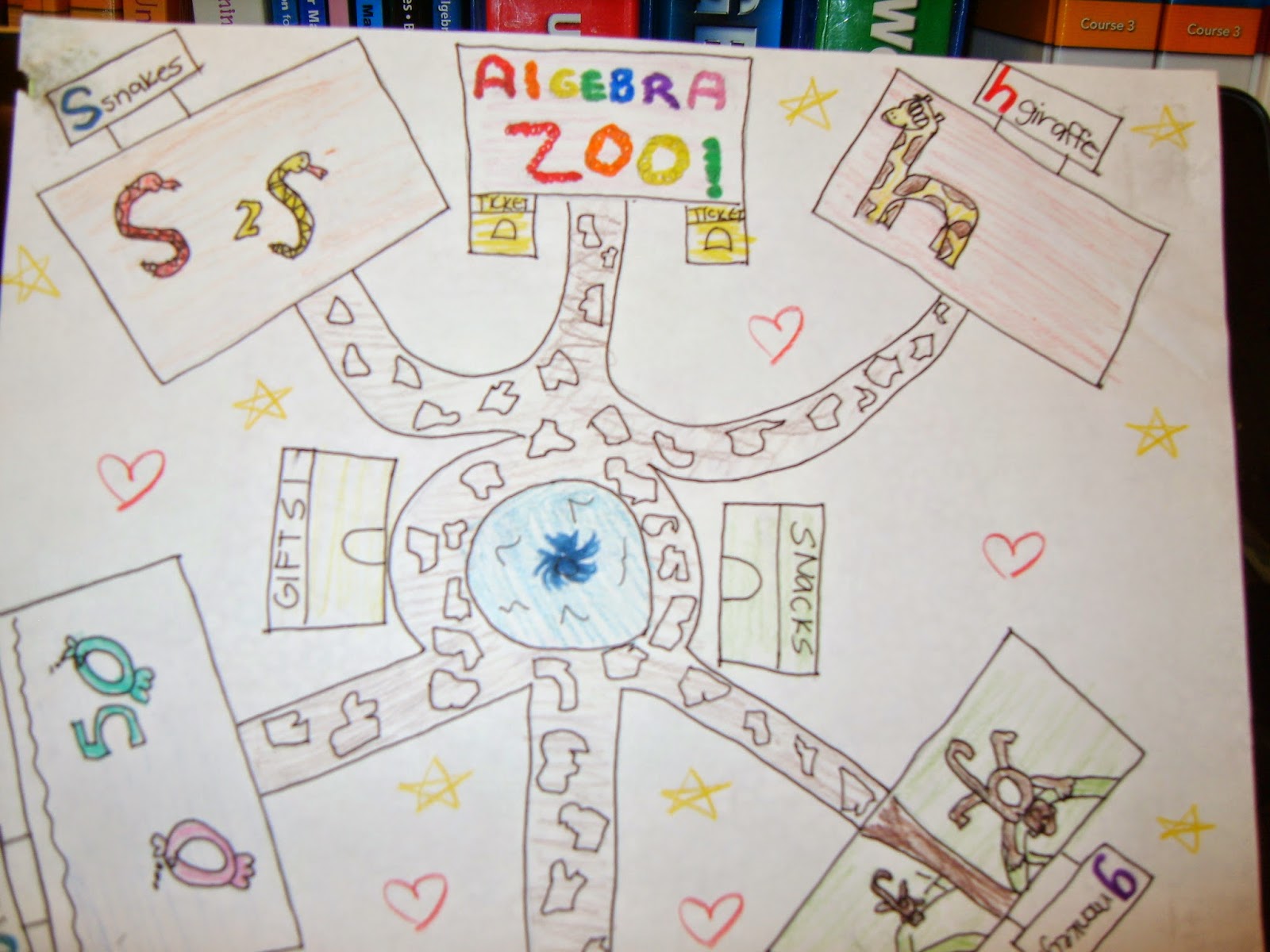I love that the monkeys are Gs!

That idea has stuck with me since 8th grade and I have told that story, or at least some version of it, to many students.  I have only been having students make pictures that we display as a reminder for the past few years.  It is silly but it really does help some students.

When I give this assignment, I ask the students to be creative.  I ask them to try and make their animals look like the variable they represent.  I expect that it is colored and neatly finished.



I also tell them that although x and x^2 look the similar, they are not the same creature and cannot be in the same cage together.  It is always interesting to see what they can come up with in their pictures.

I will admit that this is cutesy, but sometimes, cutesy just works! :)

Kahoot! is a Hoot!

So, at the end of last year, I was reading through the posts on Edmodo that other math and social studies teachers had posted.  One that caught my eye was about Kahoot!  Several teachers commented and talked about the fact that their students loved it.  I was intrigued and looked into the site.  First off, I found out that it was free which fits perfectly into my teacher budget.  Next, I found that it was super easy to use and didn't take a lot of time or work to make a review/quiz which fit into the hectic end of year schedule that I had.  Finally, I discovered that my students loved it!  It surprised me, to be quite honest.  The first group I tried it with was my least math loving students.  They were totally into it and wanted to play more.  I decided that if it could motivate my students that didn't love math, maybe it was worth using more often.

Kahoot! can be played on a computer, a laptop, an iPad, or a cell phone.  As long as you have access to an internet connection and web browser, you can play from anything.  Here is a quick walk through of Kahoot!  I took a lot of screen shots so you get a feel for the game part of the site.  I was also in the preview mode, not the full game of the literal equations review/quiz that I had made.  The cell phone is only on the side when you play a preview of a review/quiz.

First of all, Kahoot! is full of reviews/quizzes that other teachers have made and shared.  If you didn't want to make your own, chances are you will find something that you can use.  This is a screen shot of a search that I did for equations through the public reviews/quizzes that are available from other teachers.  I found a lot of reviews/quizzes that are available and I do not even have to take the time to make them! : )

When a review/quiz starts, the students are shown the game pin.  For this game, it was 50964.  Students go to kahoot.it and they will be asked to enter the pin.  Also, the pins change each time you play, so you can't just write the pin on the board and use it for every class.  Yep, I tried that and it didn't work.

 

Students are then prompted to enter a username.  I know when I do this next year, I will assign the group names to the students.  This was the most time consuming part.  As students enter their username, it appears on the screen.  When all of the students are entered, push the start now button and the review/quiz will begin.

 

The question comes up without choices to give students time to read it before the choices appear.

Then the question with the choices comes up.  On the students screen they just see the 4 boxes (red, blue, gold, and green) with the shape in each colored box.  You can set the amount of time students have to answer the question.

Kahoot! shows how the class did.  If, I remember right, the students also see if they are correct after everyone has answered on their device screen.

This screen shot just shows what it would look like if the answer was wrong.  Since I was the only one playing this game, it looks a little funny.  I liked these screens at the end of the review/quiz because if I was using it for error analysis, I could see how many students/teams in the room were making a particular mistake.  It was a quick "dipstick test" to see where understanding was.

Another feature that I like is that 2 answers can be correct.  Actually, all 4 could be correct if you wanted it to be.  In this screenshot, I had E/R=I and I=E/R as correct answers.

After the correct answer is revealed, the scoreboard is revealed.  Students really loved this!  There was a lot of motivation to do the next problem if you came in 2nd, 3rd, etc. place on the last question.  I was surprised that even my struggling students were working to solve the problems and didn't give up.  Competition was motivating!

At the end of the game, the final scoreboard is shown and students can see how they did.  I just gave the first place team eternal bragging rights, but next year, I think I will have a prize of some sort.

After the final scoreboard, there is a feedback form that students can fill in about their experience with the review/quiz.

The final screen declares the winner.  I like that it says how many right and wrong the team/individual had.  I think it helps to see that no one is perfect all the time.  Speed usually causes even the best students to mess up.

I usually don't talk about a website to this extent, but this is actually one that I am excited about and think it will be useful next year to switch things up and do something different.  

Mathematical Conversations

Mathematical conversations are a technique that I learned over a year ago, but never put it into practice.  This year I am going to give it a go and I am hoping that it helps some students solidify vocabulary and procedures.

The technique is pretty simple.  The teacher writes a script that the students will read in partners or triads.  The students then put on their best acting abilities and read the script with each other.  The script should be read through at least twice and students should change roles.  The script does not have to be long, but should be focusing on key vocabulary, procedures, or concepts that students aren't understanding.

After students are comfortable with the way a mathematical conversation should be in the class, they can try their hand at writing their own for the class to read or acted out by the authors.  It is a great way to get writing happening in the math classroom!  Student written or teacher written scripts could make a possible activity for a station.  Several scripts as stations could be a review activity as well.

My first attempt at trying to write a mathematical conversation is below this paragraph.  I picked the topic of subtracting integers because it is reviewed in the text and I know that this was hard for the kiddos last year.  As Algebra students,
they have to be comfortable with the subtracting integers.  My conversation is longer than what it should be.  In reality, it should be less than a page.  I just wanted to try and bring in some conceptual understanding too.  I am also debating if I should go with the traditional rule of "add the opposite" or stick with the "keep, change, change" rule that I went with last year.  For consistency, "keep, change, change" really is the better choice.  If the conversation would be useful to you, you are welcome to it.

Reflection on Vocabulary

Tonight, I was trying to narrow down the 28 vocabulary words in the first section of my algebra text to a more manageable 13 or 14.  I was actually having a hard time because I know that all of these words will creep up again on my students on a test produced by the text or on a homework problem.  When I looked at the 28, I was having a hard time deciding which words should be cut.

Therefore, the mess above started.  I thought if I could draw out the connections and determine the words that would be connected together the most often, I could narrow it from there.  My mess of solid lines and dashed lines started to draw a very clear picture for me.  It confirmed something that my gut had been telling me the last couple of years.  The words that I think are the most important and vital to students future math classes doesn't agree with the publisher's opinion all the time.

After creating the mess of lines,  I took out my highlighters (because every teacher has more than one) and highlighted the words in yellow that had the most connections from/to them.  The orange are words I think my students really should know for the future and are part of a standard.  I realized that there are words, like closure, that I would stress to the students because it popped up in homework and on the tests produced by the publisher.  One reason the students always struggled was due to lack of connection with the other lessons in the first section.  Closure only connects to counterexample and there should be a line up to sets.  Other vocabulary can be connected to other terms in other contexts.

Looking at this mess of lines, I am realizing that this might actually be a really good activity to do with students.  I could start a flip chart on my interactive white board and we could revisit it after every lesson and add the new vocabulary and draw the connections on the board.  Students could also keep an ongoing chart in their INBs.  I am thinking through my keyboard right now, but I am starting to see some possibility here.

Does anyone have a good way of narrowing vocabulary?  Love to hear your ideas!